计算机图形学02

Transform（变换），图形的变换

1
2
3
4
5
为什么学习变换
2维变换：旋转、缩放、切变
齐次坐标 Homogeneous coordinates
组合变换
3维变换

二维变换

将矩阵和变换联系起来

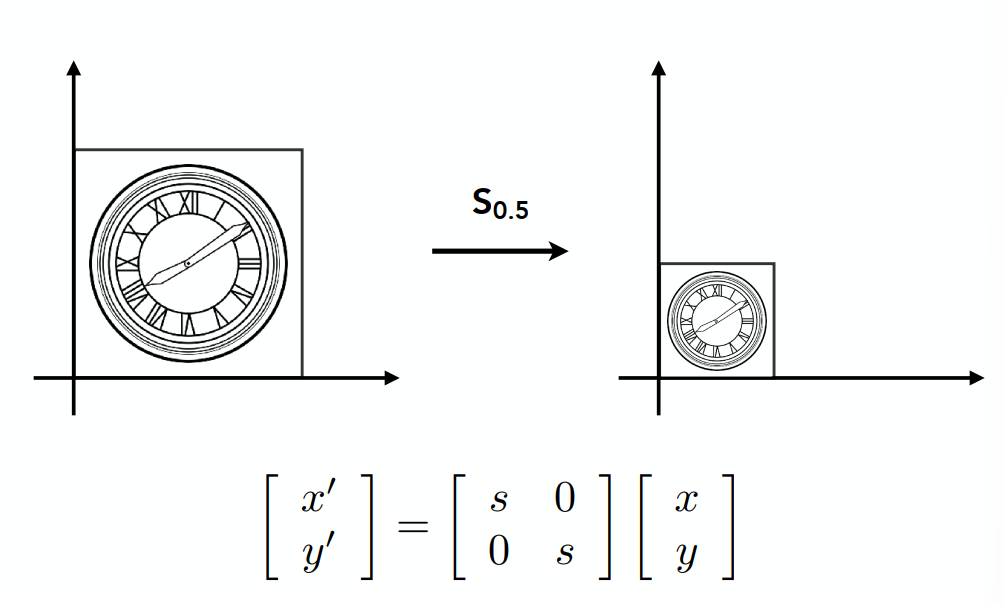
  • 1、缩放

    将坐标在向量左边乘一个对角矩阵

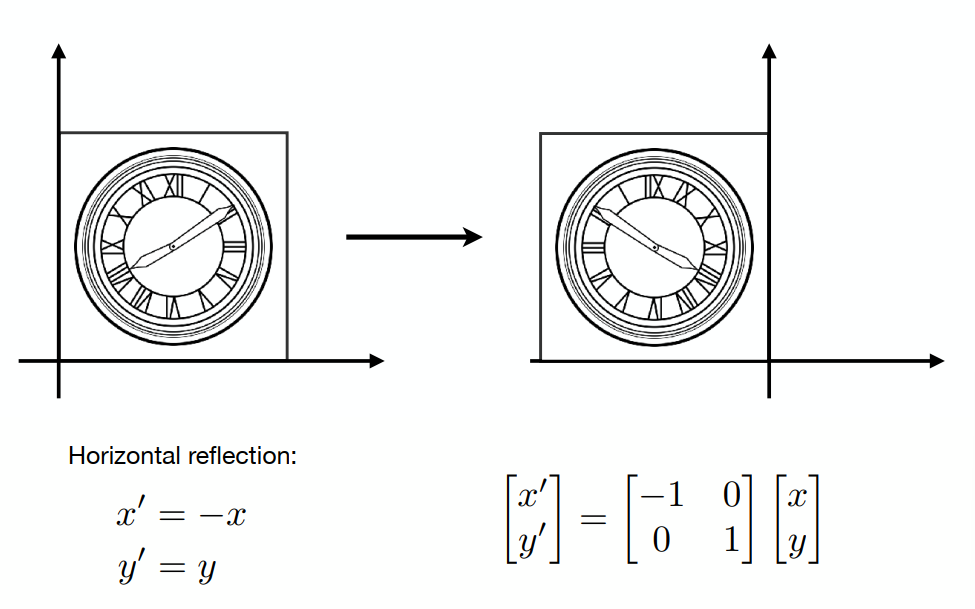
  • 2、反射对称

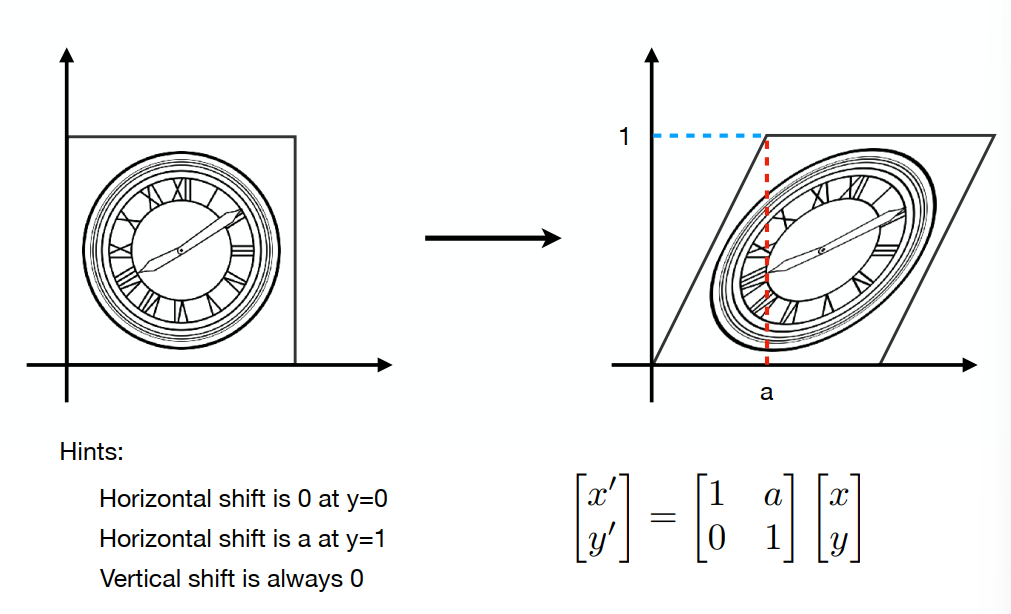
  • 3、切变（Shear Matrix）

    水平方向坐标发生改变，竖直方向不变，水平的移动大小，按照Y的当前坐标成正比

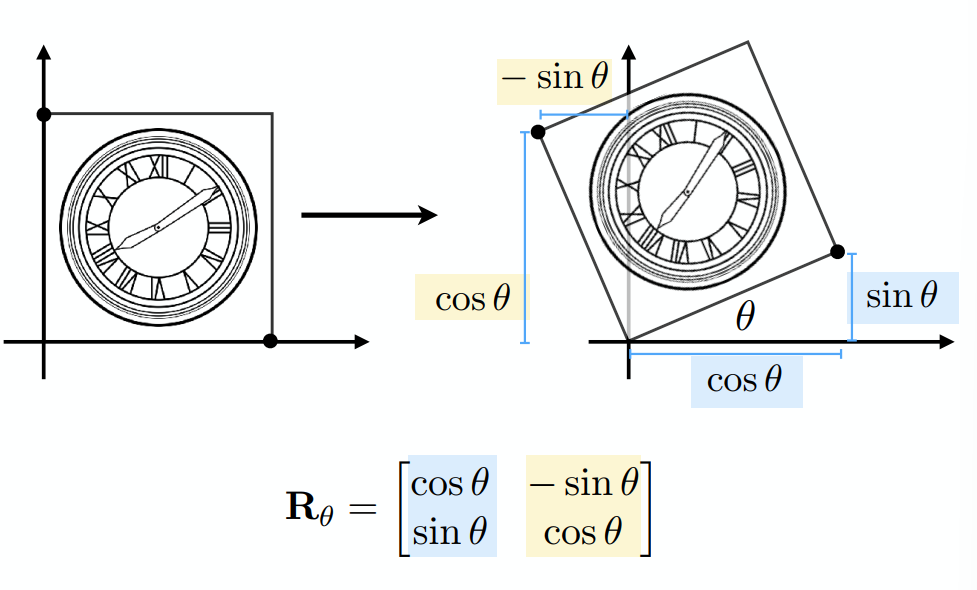
  • 4、旋转

    .PNG)

通过矩阵乘积可以将一个输入图形的坐标转化为想要的输出矩阵的坐标，这样的变换都称为线性变换

齐次坐标（homogeneous coordinates）

平移操作无法使用线性变化即矩阵的乘法来获得，所以引入齐次坐标，增加一个维度

齐次坐标的矩阵操作，可以叫做仿射变换

增加维度以后，通过与新增加列的运算就可以达到平移的变换

  • Q：Why？将二维的点，增加一个1，将二维的向量，增加一个0

    1、通过增加的维度可以标识当前的坐标表示点还是表示向量。可以保证向量具有平移不变性

    2、最后一个维度的运算正好表示运算结果的性质

    3、点+点，得到的结果为两个点的终点，因为第三维为2，与两点之和相除便是中点

齐次坐标下的变换操作矩阵

  • 逆变换

    乘以变化矩阵的逆矩阵，可以变换成原来的图片

变换组合

1、复杂变换可以通过简单的变化来得到

2、变换的顺序不同，得到的结果不同

3、变换的组合，等价于原始矩阵依次乘上按照一定顺序的齐次矩阵

  • 将一个变化还原，或者以任意一个点为中心进行变化，可以先移动到原点，再进行操作

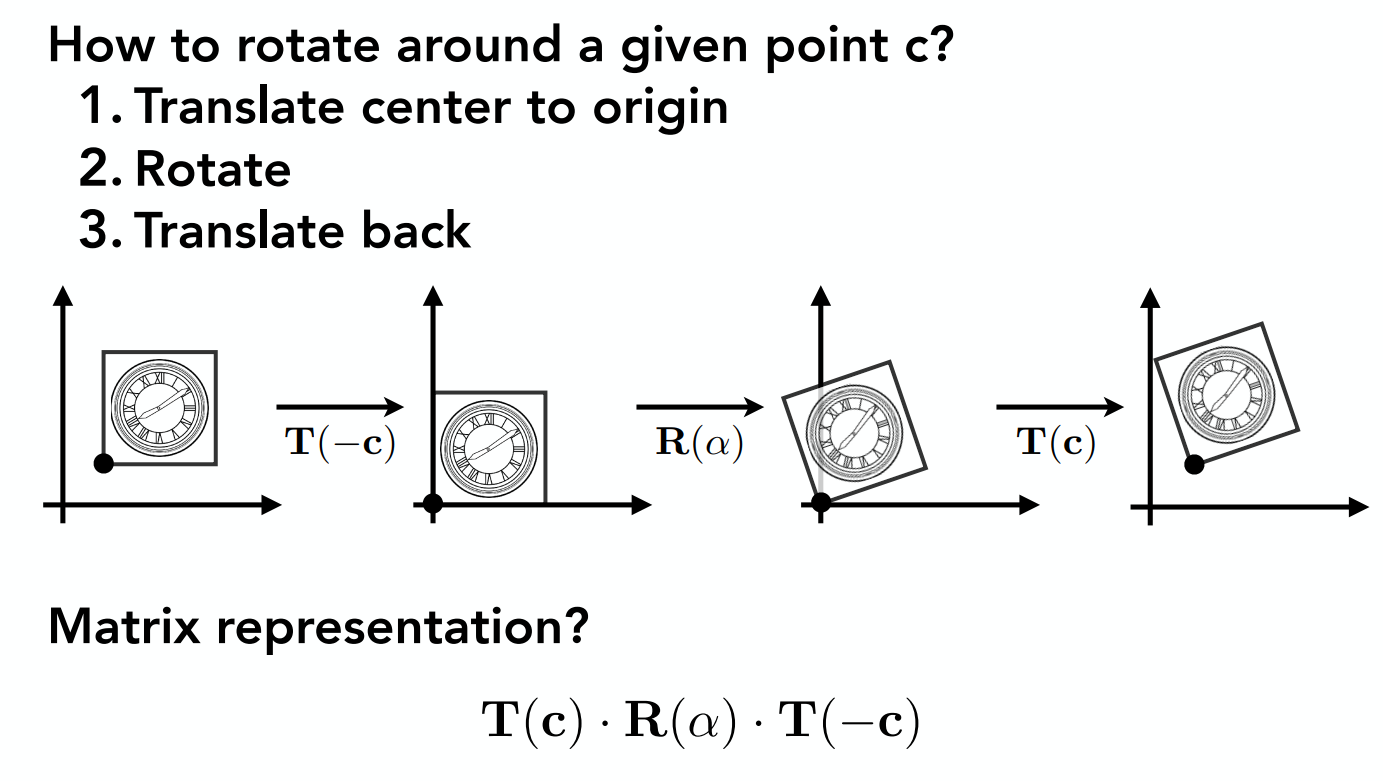
三维变换

  • 三维点和三维向量

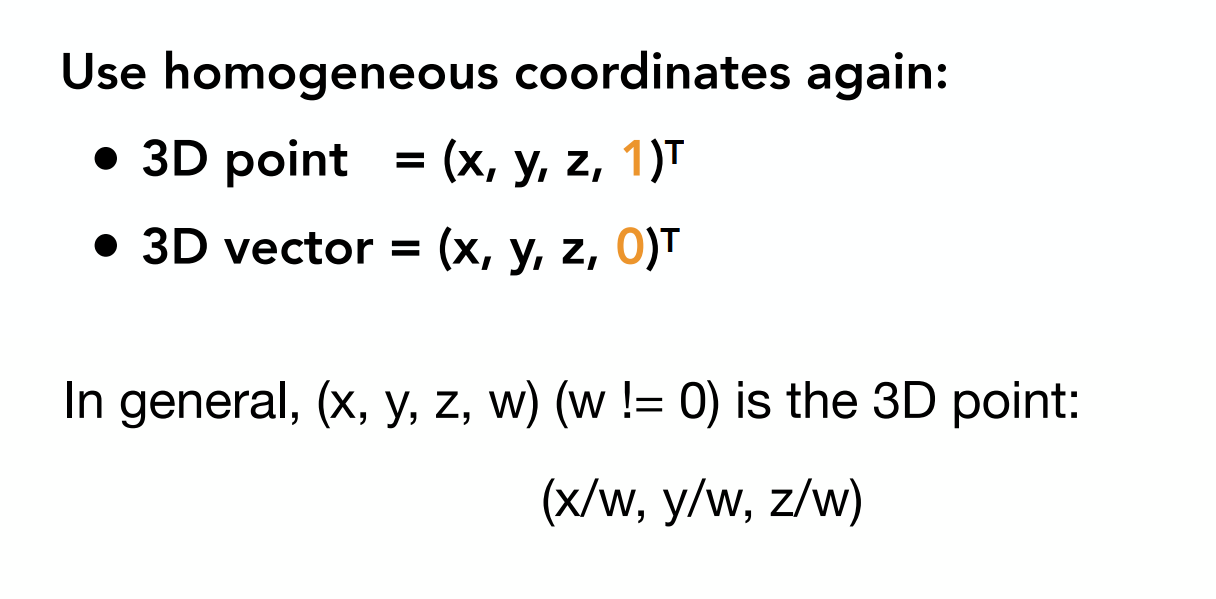
  • 三维变换齐次矩阵

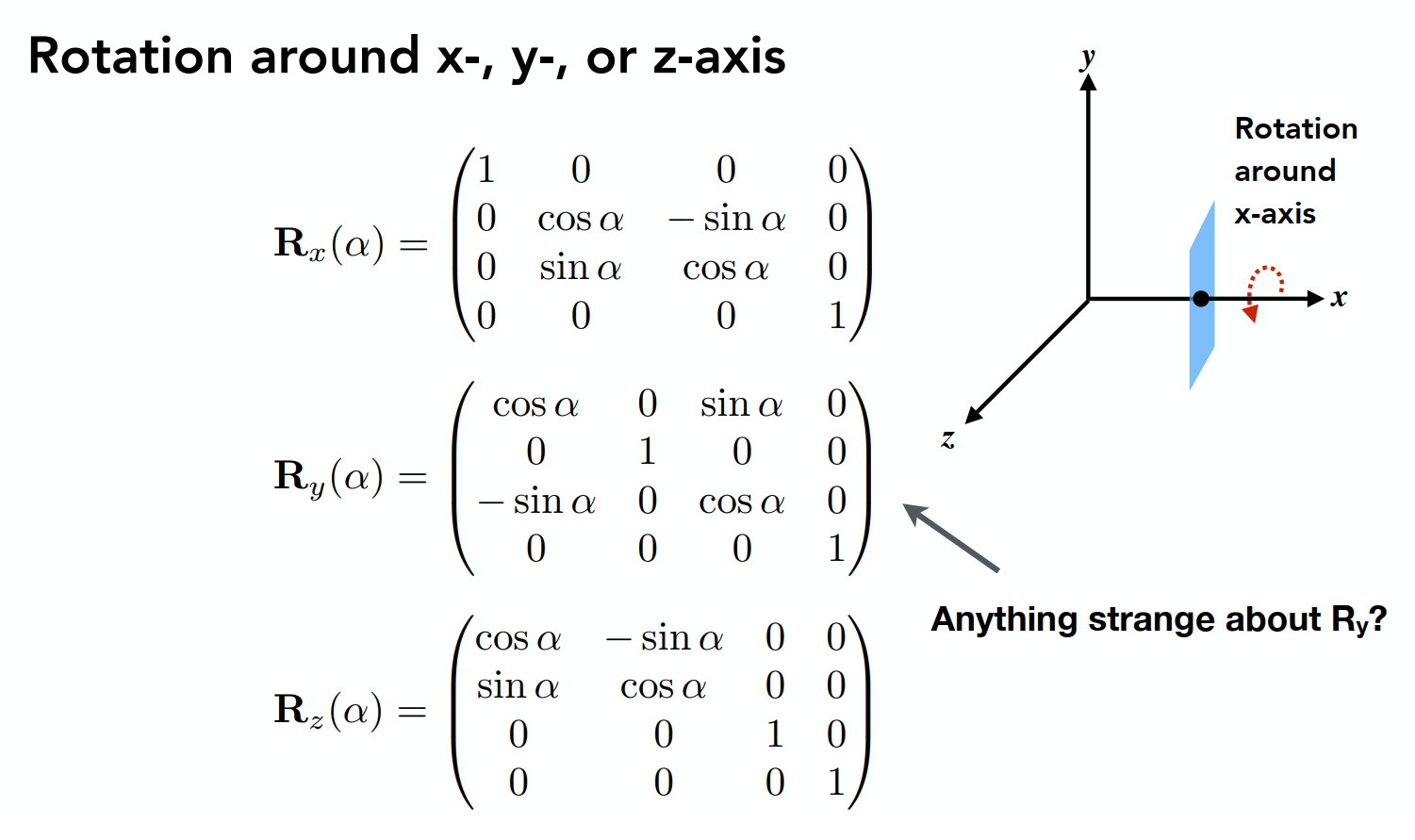
  • 旋转

    绕哪个轴旋转哪个轴保持不变

    对于一般性的旋转，可以使用简单旋转的组合来完成

  • 使用旋转公式

    旋转角度定义为a

    旋转轴定义为n

    其中I表示为单位矩阵

    表示为，沿着旋转轴n旋转a的角度得到的旋转矩阵

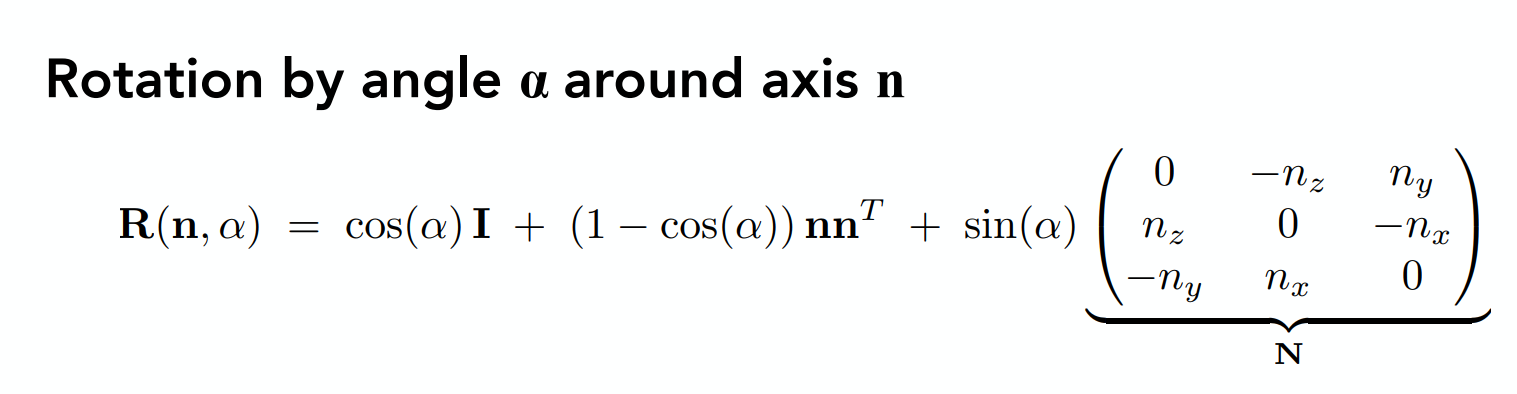
观测变换（Viewing transformation）

视图变换、投影变换（正交投影，透视投影）