计算机图形学01

应用场景：电影，动画，可视化，家具，模拟，虚拟现实（VR），GUI（图形用户接口），字体

  • 好的画面：足够亮（全局光照）
1
2
3
4
1、光栅化	Resterization
2、曲线曲面（几何）	Curves and Meshes
3、光线追踪	Ray	Tracing
4、动画/模拟	Animation/Simulation

计算机图形学 VS 计算机视觉

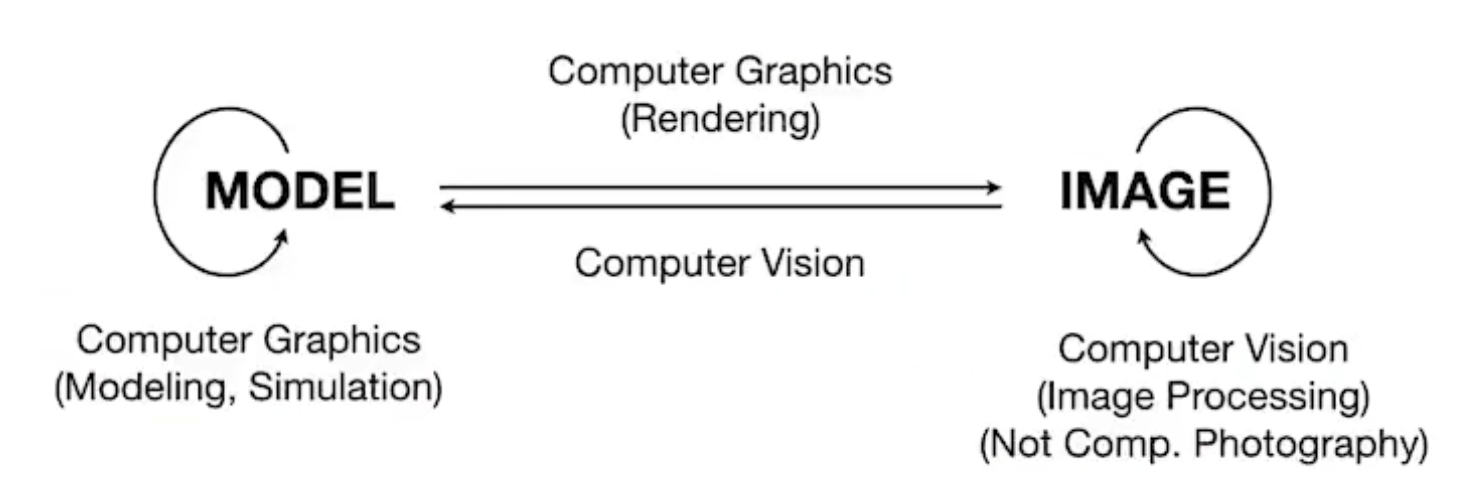
  • MODEL，计算机画（图形学）

    正向箭头：将三维空间的图形在二维中展示出来，特指图像渲染

    自我箭头：MODEL的自我渲染，与图像无关

  • IMAGE，计算机看（计算机视觉）

    反向箭头：从图形中推导和识别出图像的特征

    自我箭头：依赖深度学习对图像进行处理

作业相关

1
2
3
1、作业链接：http://games-cn.org/forums/topic/allhw/
2、作业使用的系统：smartchair
3、Use IDE：集成开发环境

线性代数——A Swift and Brutal Introduction to Linear Algebra

数学：线性代数，微积分，统计，物理：光学，力学，信号处理，数值分析

向量Vectors

方向、长度、向量的模、单位向量、点乘、余弦值

  • 点乘的重要性

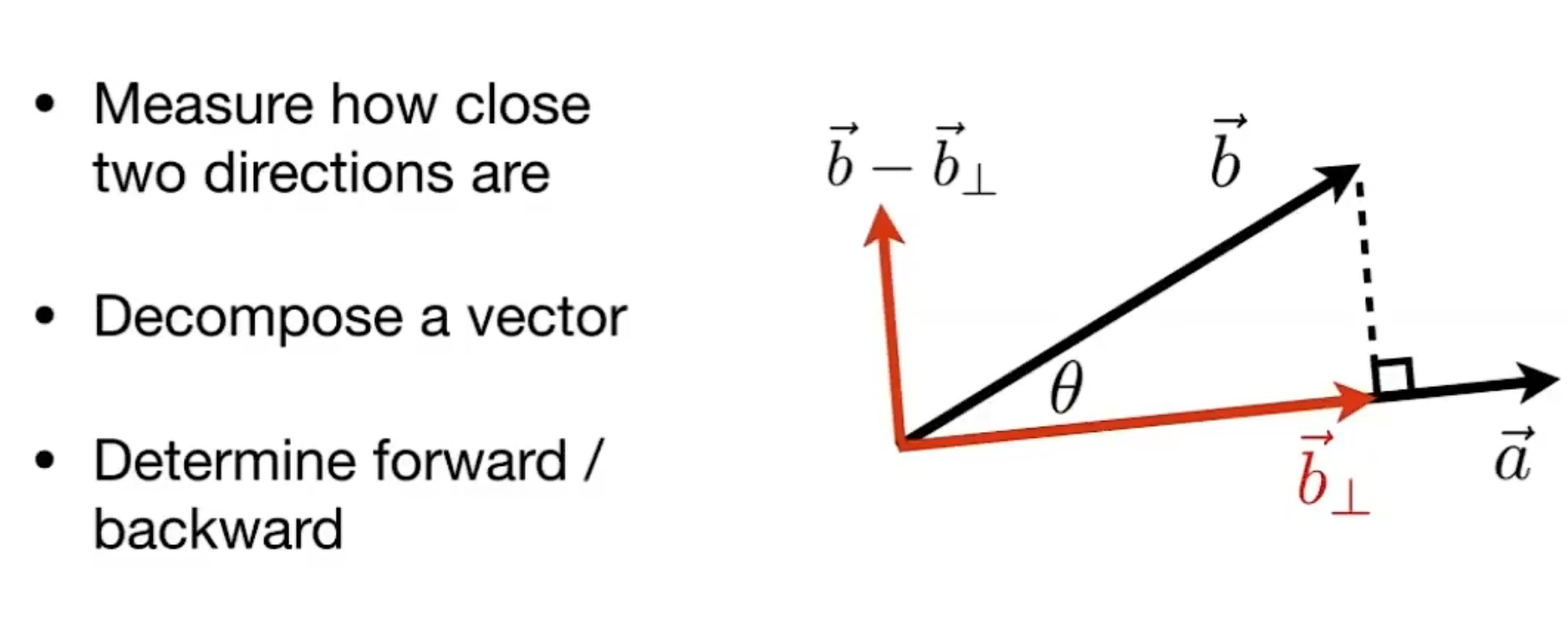
    使用向量的点积便于计算一个向量在另一个向量上的投影（光的投影）

    衡量两个向量的接近程度

    分解一个向量（使用投影可以进行加减运算）分解为垂直方向和水平方向

    确定向量的基本方向，大于零同方向，小于零反方向

  • 叉乘的重要性（使用右手螺旋定则可以确定叉乘的方向）

    叉乘可以建立一个三位空间的直角坐标系

    任意的三维空间向量都可以分解到三位的单位向量中

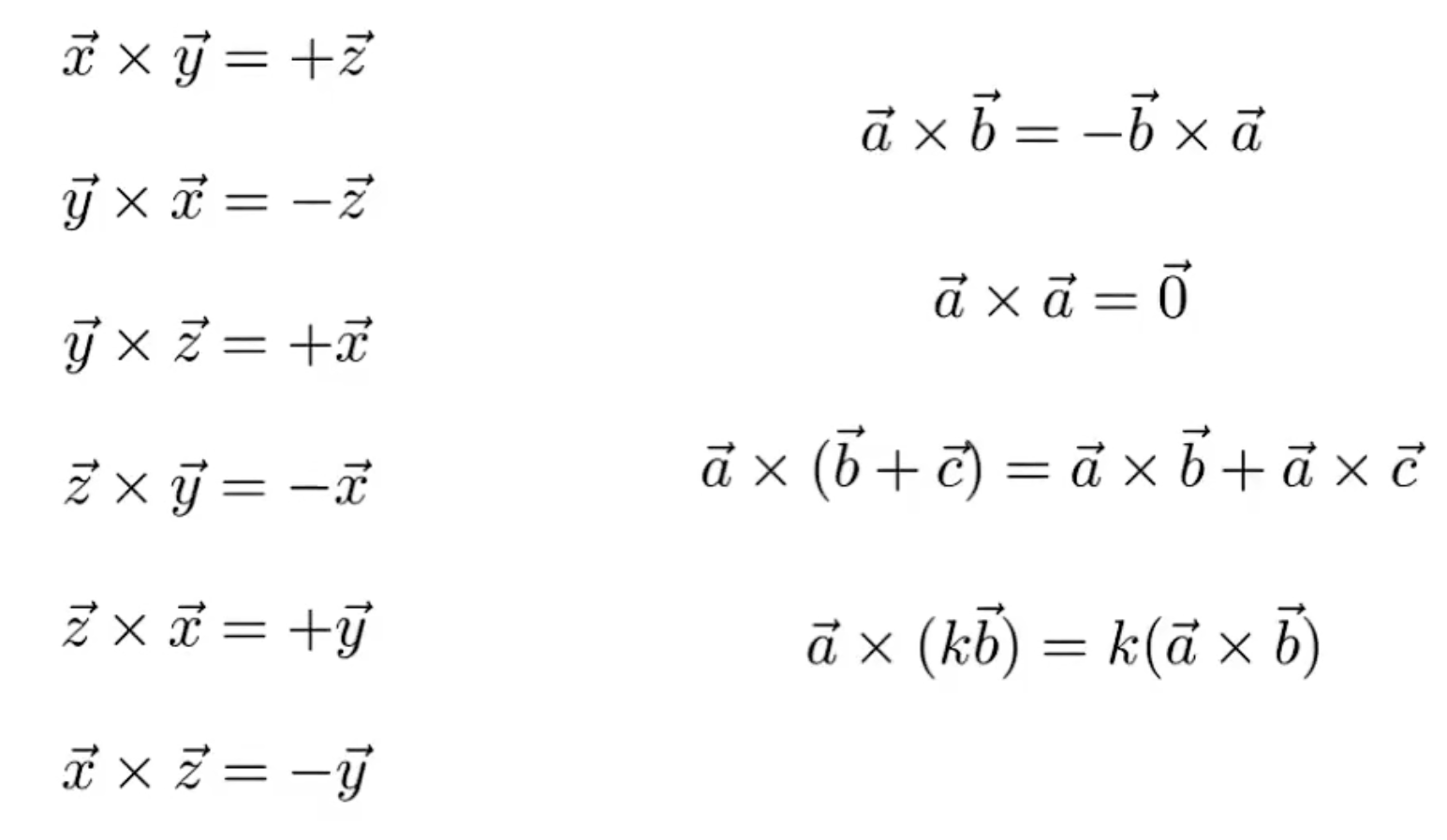
​ 叉乘的代数表示（矩阵相乘）

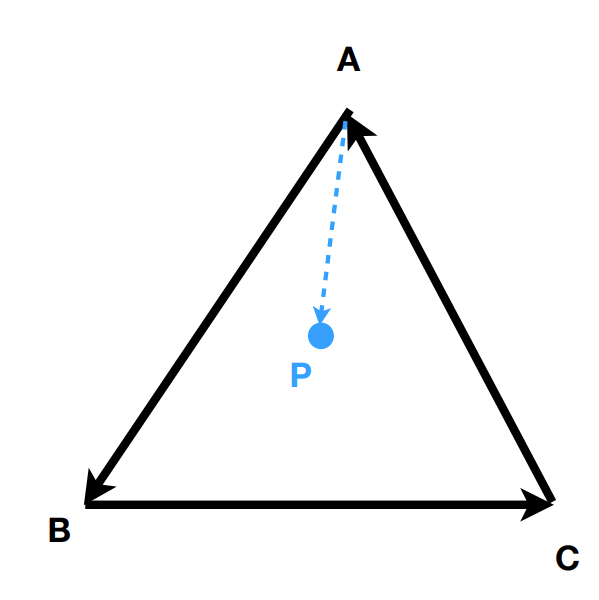
Q&A:判断一个点是否在三角形的内部

对三角形做逆时针，分别做三条边之间的向量，三个顶点分别于需要判断的点进行叉乘，如AB叉乘AP，如果都大于0，则说明在三角形内部。

结论比较简单，很容易在计算机中使用公式实现出来。

  • 矩阵的重要性

    图像转换，旋转，平移，剪切，数乘

    • 矩阵的乘积（第一个矩阵的列数等于第二个矩阵的行数）

      矩阵的乘积没有任何交换律，但是有结合律

    • 矩阵与向量的乘积（列向量，可以表示为点的坐标）

      可以利用矩阵乘积做一些变化操作（如下：将x，y变化为-x，y）

    • 转置矩阵、单位矩阵（对角矩阵）