实验一、线性回归

  • 已知模型y = a*x + b
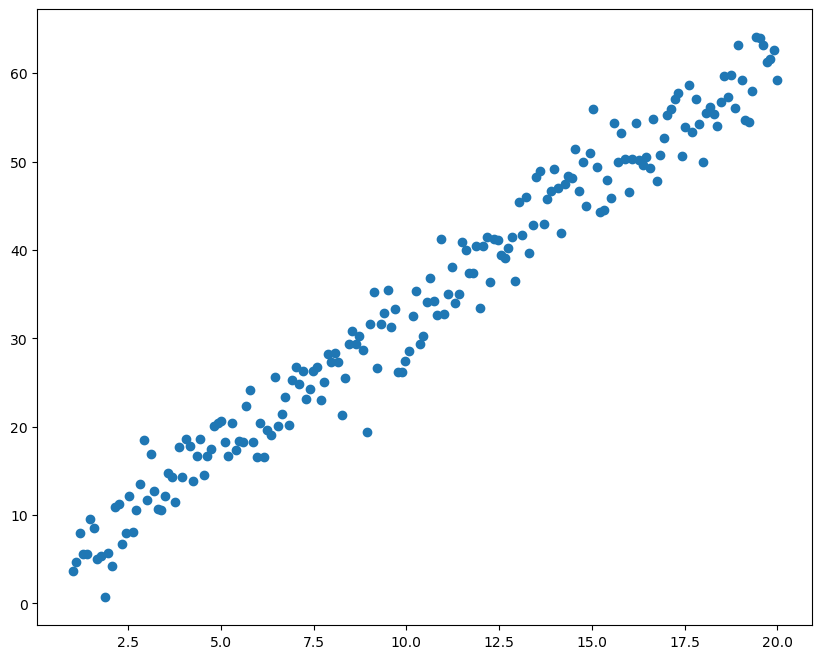
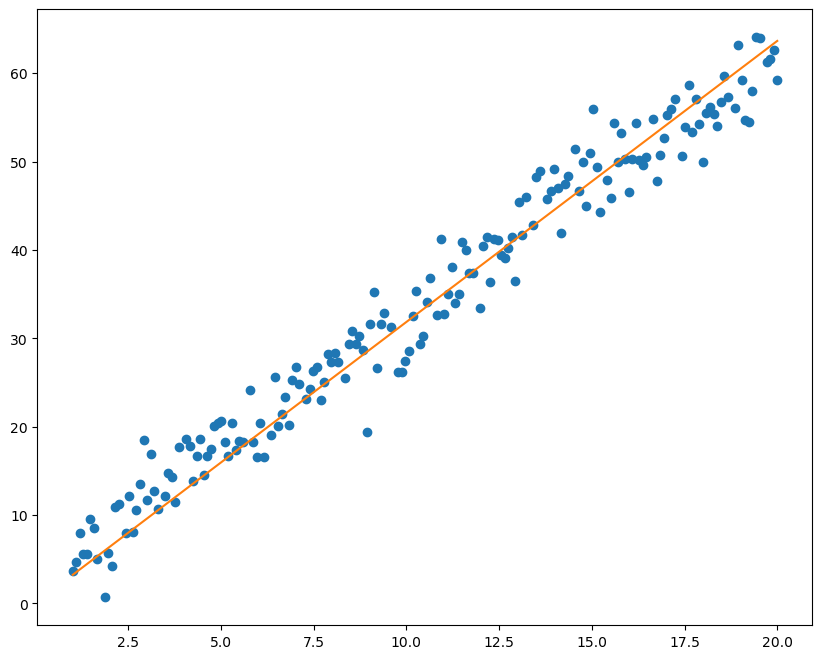
  • 生成带噪声的数据拟合线性函数
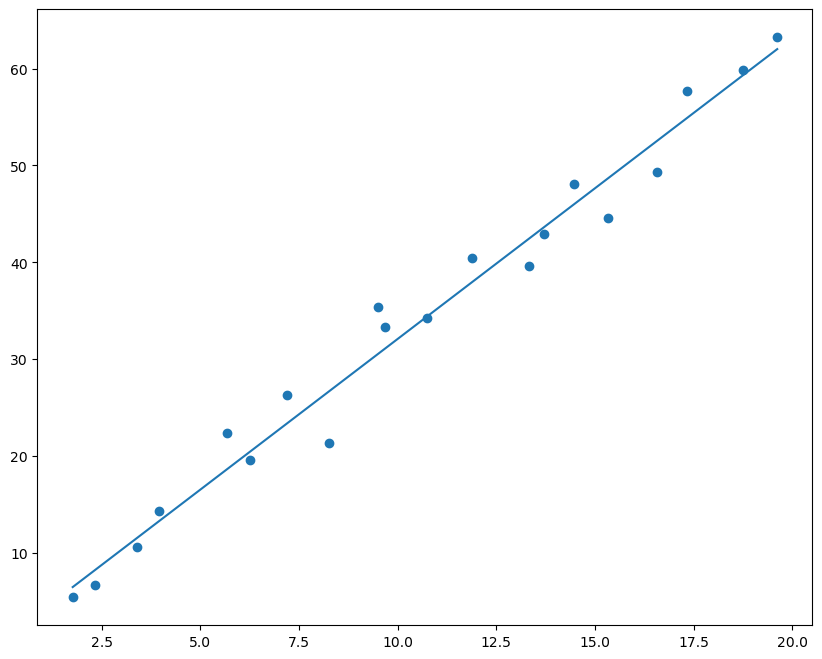
  • 绘制图像拟合效果
1
2
3
4
5
# 导入相关包
import torch
import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt
1
2
3
4
5
6
7
# 生成y = a*x + b的噪声数据200个
# 定义a = 3， b = 2
a, b = 3, 2

x_datas = torch.linspace(1,20,200)
rand_noise = torch.randn(200)*3
y_lables = a*x_datas + b + rand_noise
1
2
3
4
# 绘制散点图
plt.figure(figsize=(10, 8))
plt.scatter(x_datas, y_lables)
plt.show()

​

​ 

1
2
3
4
5
6
7
8
# 将数据划分为训练集和测试集，按照180，20进行划分
# 每十个数据中，分层抽取出一个数据作为测试集

test_index = [10*i + np.random.randint(10) for i in range(20)]
train_index = [i for i in range(200) if i not in test_index]

X_train1, X_test1, y_train1, y_test1 = x_datas[train_index], x_datas[test_index], y_lables[train_index], y_lables[test_index]
y_train1
tensor([ 3.6945,  4.7438,  7.9504,  5.5705,  5.6000,  9.5666,  8.5461,  4.9789,
         0.6976,  5.6866,  4.2295, 10.9321, 11.2976,  7.9842, 12.1275,  8.0943,
        10.5445, 13.4849, 18.5069, 11.6880, 16.8814, 12.7575, 10.7111, 12.1603,
        14.7055, 14.3254, 11.4367, 17.6528, 18.5793, 17.8409, 13.8733, 16.6622,
        18.6143, 14.5482, 16.6509, 17.4552, 20.0250, 20.3924, 20.6348, 18.2929,
        16.6831, 20.4449, 17.3773, 18.3895, 18.2360, 24.1661, 18.2511, 16.6143,
        20.3642, 16.5544, 19.0061, 25.6141, 20.1254, 21.4796, 23.3279, 20.1736,
        25.3058, 26.7936, 24.8702, 23.0888, 24.2360, 26.3334, 26.8100, 22.9726,
        25.0721, 28.1969, 27.3128, 28.3941, 27.2811, 25.5293, 29.3596, 30.8378,
        29.3787, 30.2246, 28.6970, 19.3994, 31.6431, 35.1937, 26.6844, 31.5928,
        32.8604, 31.2751, 26.1607, 26.1867, 27.4753, 28.5589, 32.5150, 35.3546,
        29.3716, 30.2867, 34.1565, 36.8429, 32.5876, 41.2268, 32.7979, 35.0479,
        38.0979, 34.0405, 35.0074, 40.8656, 39.9885, 37.4418, 37.3445, 33.4271,
        40.4349, 41.4754, 36.4292, 41.2385, 41.1300, 39.4304, 39.1217, 40.2641,
        41.4882, 36.4677, 45.3880, 41.7064, 46.0084, 42.7886, 48.2276, 48.9552,
        45.7761, 46.6802, 49.1144, 47.0020, 41.9040, 47.4266, 48.3905, 51.4273,
        46.7154, 49.9467, 45.0021, 50.9472, 55.9469, 49.3655, 44.3413, 47.9426,
        45.9358, 54.3920, 49.9636, 53.2459, 50.3228, 46.5756, 50.2442, 54.3946,
        50.2086, 49.6290, 50.5312, 54.7947, 47.7757, 50.7428, 52.6791, 55.2901,
        55.9978, 57.0760, 50.6741, 53.8824, 58.6424, 53.3195, 57.1432, 54.2989,
        49.9915, 55.4631, 56.1260, 55.4143, 54.0111, 56.7517, 59.6828, 57.2633,
        56.1236, 63.1750, 59.2744, 54.7133, 54.5091, 57.9472, 64.0721, 63.9801,
        61.2980, 61.6411, 62.6100, 59.2035])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 将训练集转化为张量，使用梯度下降法进行训练
# 迭代次数 10000，学习率：0.001

a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
loss = []
theta = 0.00001

for i in range(10000+1):
    y_p = a.expand_as(X_train1)*X_train1 + b.expand_as(X_train1)
    loss_tmp = torch.mean((y_p - y_train1)**2)
    if i%500 == 0:
        print("迭代" , i , "次，损失值为：",loss_tmp.data.numpy())
    
    loss.append(loss_tmp.data.numpy())
    loss_tmp.backward()
    a.data = a.data - theta*a.grad.data
    b.data = b.data - theta*b.grad.data
    a.grad.data.zero_()
    b.grad.data.zero_()
    
print(a, b)
迭代 0 次，损失值为： 1019.3526
迭代 500 次，损失值为： 68.77335
迭代 1000 次，损失值为： 12.962891
迭代 1500 次，损失值为： 9.682995
迭代 2000 次，损失值为： 9.4870615
迭代 2500 次，损失值为： 9.47218
迭代 3000 次，损失值为： 9.467946
迭代 3500 次，损失值为： 9.46435
迭代 4000 次，损失值为： 9.460806
迭代 4500 次，损失值为： 9.457279
迭代 5000 次，损失值为： 9.453774
迭代 5500 次，损失值为： 9.450276
迭代 6000 次，损失值为： 9.446788
迭代 6500 次，损失值为： 9.44333
迭代 7000 次，损失值为： 9.439879
迭代 7500 次，损失值为： 9.436436
迭代 8000 次，损失值为： 9.433018
迭代 8500 次，损失值为： 9.429613
迭代 9000 次，损失值为： 9.426218
迭代 9500 次，损失值为： 9.422838
迭代 10000 次，损失值为： 9.419481
tensor([3.1121], requires_grad=True) tensor([0.9682], requires_grad=True)

1
2
3
4
5
6
plt.figure(figsize=(10, 8))
plt.scatter(X_test1, y_test1)

plt.plot(X_test1.data.numpy(), a.data.numpy()*X_test1.data.numpy() + b.data.numpy())

plt.show()
  • 已知模型y = ax^3 + bx^2 + c*x + d
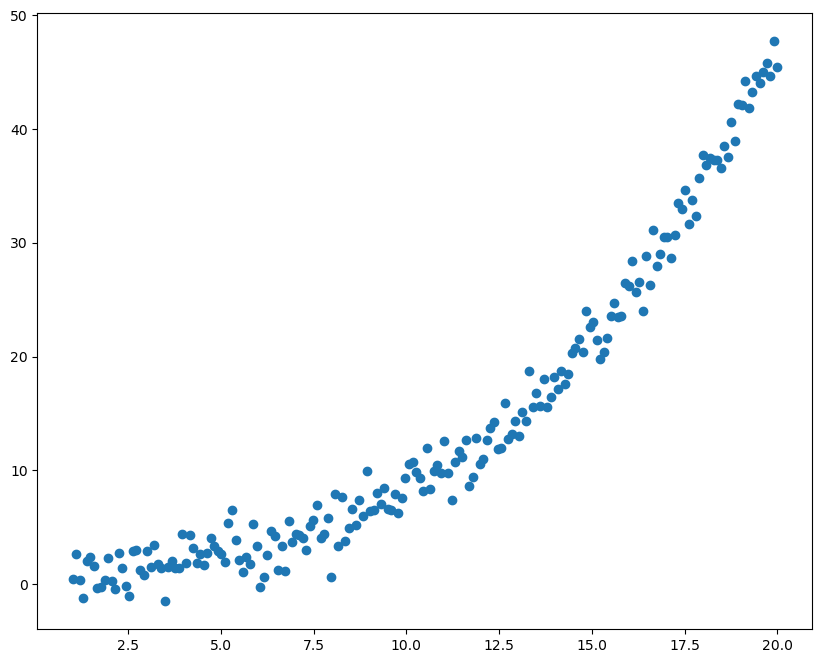
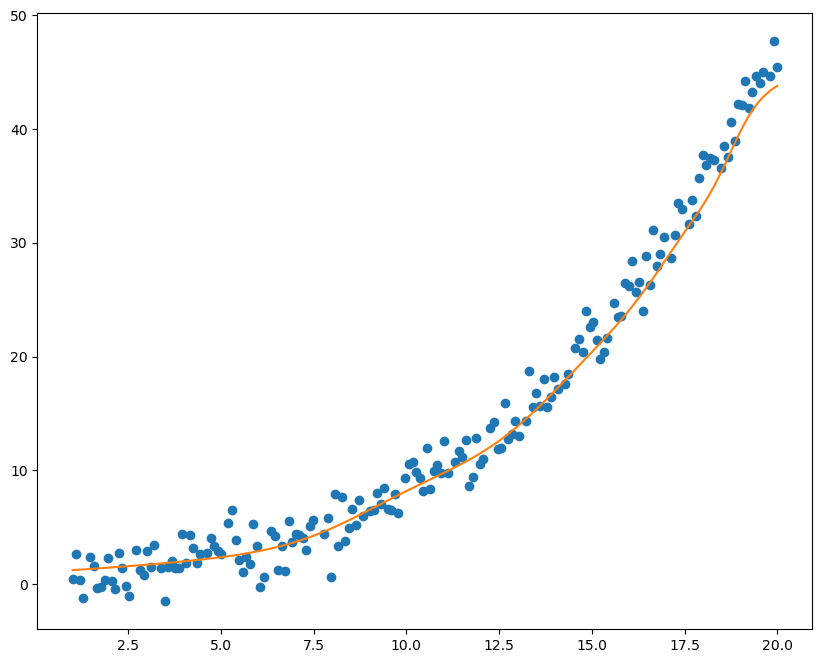
  • 生成带噪声的数据拟合三次函数
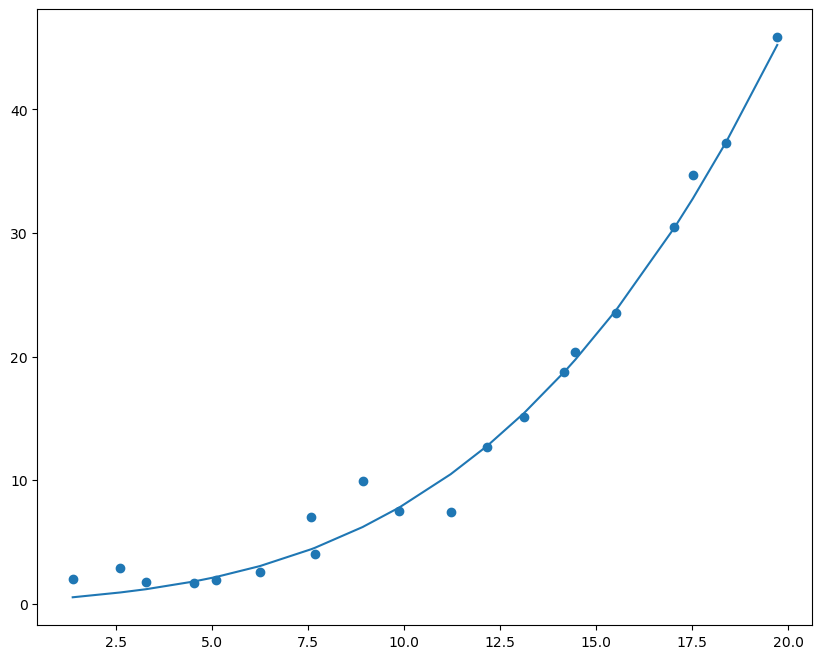
  • 绘制图像拟合效果
1
2
3
4
5
6
7
8
9
10
11
12
# 生成200个噪声数据
# 参数设置，a=0.005, b=0.01, c=0.1, d=1

a, b, c, d = 0.005, 0.01, 0.1, 1

rand = torch.randn(200)*1.5
X_trains = torch.linspace(1, 20, 200)
Y_labels = a*(X_trains**3) + b*(X_trains**2) + c*X_trains + d + rand

plt.figure(figsize=(10, 8))
plt.scatter(X_trains, Y_labels)
plt.show()

​

​ 

1
2
3
4
5
6
# 构造数据集和训练集标签

test_index = [10*i + np.random.randint(10) for i in range(20)]
train_index = [i for i in range(200) if i not in test_index]

X_train2, X_test2, y_train2, y_test2 = X_trains[train_index], X_trains[test_index], Y_labels[train_index], Y_labels[test_index]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 开始训练
a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
c = torch.rand(1, requires_grad=True)
d = torch.rand(1, requires_grad=True)
theta = 0.0000001
times = 50000
loss = []

for i in range(times+1):
    loss_tmp = torch.mean(((a.expand_as(X_train2) * (X_train2**3) + 
                           b.expand_as(X_train2) * (X_train2**2) + c.expand_as(X_train2) * X_train2 + 
                           d.expand_as(X_train2) - y_train2))**2)
    if i%2500 == 0:
        print("迭代", i,"次，损失值为：", loss_tmp.data.numpy())
    
    loss_tmp.backward()
    a.data = a.data - a.grad.data * theta
    b.data = b.data - b.grad.data * theta
    c.data = c.data - c.grad.data * theta
    d.data = d.data - d.grad.data * theta
    
    a.grad.data.zero_()
    b.grad.data.zero_()
    c.grad.data.zero_()
    d.grad.data.zero_()
    
迭代 0 次，损失值为： 3153.991
迭代 2500 次，损失值为： 11.566195
迭代 5000 次，损失值为： 5.8502893
迭代 7500 次，损失值为： 3.6634474
迭代 10000 次，损失值为： 2.8267233
迭代 12500 次，损失值为： 2.506517
迭代 15000 次，损失值为： 2.3839154
迭代 17500 次，损失值为： 2.3369095
迭代 20000 次，损失值为： 2.318825
迭代 22500 次，损失值为： 2.3118067
迭代 25000 次，损失值为： 2.3090246
迭代 27500 次，损失值为： 2.307857
迭代 30000 次，损失值为： 2.307303
迭代 32500 次，损失值为： 2.3069975
迭代 35000 次，损失值为： 2.3067696
迭代 37500 次，损失值为： 2.306577
迭代 40000 次，损失值为： 2.3063998
迭代 42500 次，损失值为： 2.3062305
迭代 45000 次，损失值为： 2.3060641
迭代 47500 次，损失值为： 2.3058996
迭代 50000 次，损失值为： 2.3057368

1
2
3
4
5
6
7
# 对测试集进行预测拟合
plt.figure(figsize=(10, 8))
plt.scatter(X_test2, y_test2)

plt.plot(X_test2.data.numpy(), a.data.numpy()*(X_test2.data.numpy()**3) + b.data.numpy()*(X_test2.data.numpy()**2) + c.data.numpy()*X_test2.data.numpy() + d.data.numpy())

plt.show()

​

​

设计神经网络对前面的数据进行拟合

  • 记录误差，绘制拟合效果
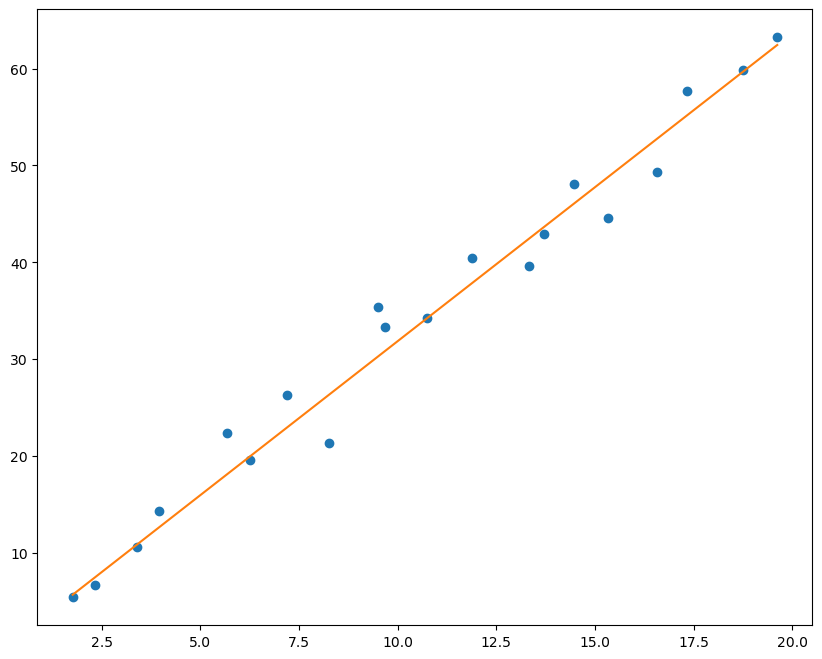
  • 直线拟合数据为：X_train1, y_train1, X_test1, y_test1
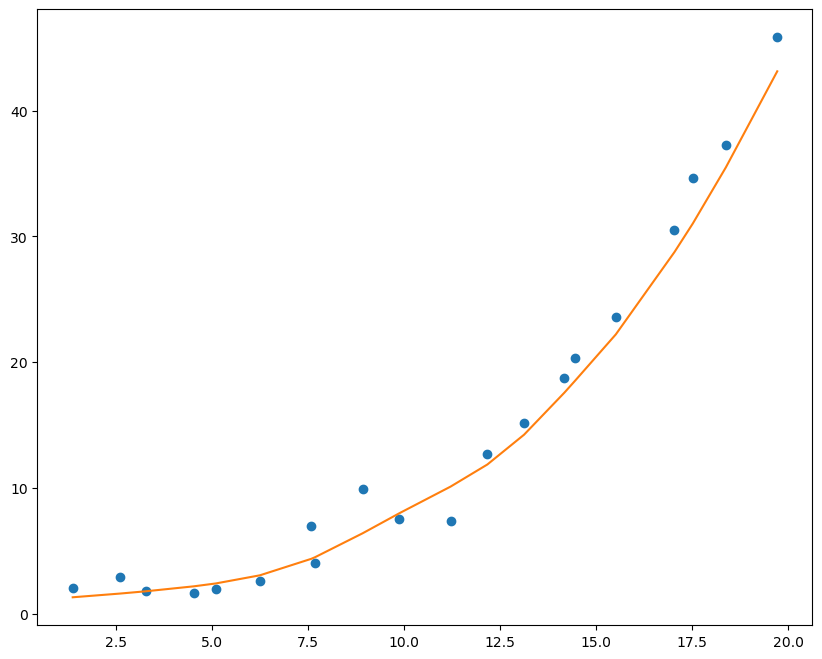
  • 曲线拟合数据为：X_train2, y_train2, X_test2, y_test2

一、拟合直线

1
2
3
4
5
6
7
8
9
10
11
# 使用网络拟合直线
# 直线拟合只需要一个神经元就能完成拟合

# 定义网络
net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
)
# 定义损失函数
loss_fn = torch.nn.MSELoss()
# 梯度下降方法，随机梯度下降
opt = torch.optim.SGD(net.parameters(), lr=0.0001)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 训练数据
losses = []
for i in range(1000):
    pred = net(X_train1.view(-1,1))
    loss = loss_fn(pred, y_train1.view(-1,1))
    if i%200==0:
        print('loss:', loss.data)
        losses.append(loss.data)
    
    opt.zero_grad()
    loss.backward()
    opt.step()
    
plt.figure(figsize=(10, 8))
plt.plot(X_train1.data.numpy(), y_train1.data.numpy(), 'o')
plt.plot(X_train1.data.numpy(), net(X_train1.view(-1,1)).data.numpy())
plt.show()
loss: tensor(999.4984)
loss: tensor(10.4790)
loss: tensor(10.4377)
loss: tensor(10.4070)
loss: tensor(10.3768)

1
2
3
4
5
6
# 对测试集进行预测验证
pred = net(X_test1.view(-1,1))
plt.figure(figsize=(10, 8))
plt.plot(X_test1.data.numpy(), y_test1.data.numpy(), 'o')
plt.plot(X_test1.data.numpy(), pred.data.numpy())
plt.show()

​

​

二、拟合多项式函数

  • 单层神经网络只能够拟合直线
  • 对多项式函数的拟合需要多层神经网络，且需要激活函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 定义model类
import torch.nn as nn
import torch.nn.functional as F

# 继承nn.Module
class model(nn.Module):
    def __init__(self):
        super().__init__()
        # 第一个隐藏层
        self.hidden1=nn.Linear(1,4)
        # 第二个隐藏层
        self.hidden2=nn.Linear(4,4)
        # 第三个隐藏层
        self.hidden3=nn.Linear(4,4)
        # 输出层
        self.out=nn.Linear(4,1)
    
    # 定义网络前向运算
    def forward(self, x):
        x = self.hidden1(x)
        x = F.sigmoid(x)
        x = self.hidden2(x)
        x = F.sigmoid(x)
        x = self.hidden3(x)
        x = F.sigmoid(x)
        x = self.out(x)
        return x
    
net = model()
print(net)
model(
  (hidden1): Linear(in_features=1, out_features=4, bias=True)
  (hidden2): Linear(in_features=4, out_features=4, bias=True)
  (hidden3): Linear(in_features=4, out_features=4, bias=True)
  (out): Linear(in_features=4, out_features=1, bias=True)
)

1
2
3
# 定义损失函数
loss_fn = torch.nn.MSELoss()
opt = torch.optim.SGD(net.parameters(), lr=0.001)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 训练数据
losses2 = []
for i in range(50000):
    pred = net(X_train2.view(-1,1))
    loss = loss_fn(pred, y_train2.view(-1,1))
    if i%2500==0:
        print('loss:', loss.data)
        losses2.append(loss)
    
    opt.zero_grad()
    loss.backward()
    opt.step()

# 绘制图像
plt.figure(figsize=(10, 8))
plt.plot(X_train2.data.numpy(), y_train2.data.numpy(), 'o')
plt.plot(X_train2.data.numpy(), net(X_train2.view(-1,1)).data.numpy())
plt.show()
loss: tensor(357.9143)


D:\02_soft\anaconda3\envs\pytorch\lib\site-packages\torch\nn\functional.py:1960: UserWarning: nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.
  warnings.warn("nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.")


loss: tensor(146.0952)
loss: tensor(23.4380)
loss: tensor(16.6693)
loss: tensor(12.3312)
loss: tensor(10.4051)
loss: tensor(8.9617)
loss: tensor(7.7465)
loss: tensor(6.7640)
loss: tensor(5.9918)
loss: tensor(5.4033)
loss: tensor(4.9512)
loss: tensor(4.5902)
loss: tensor(4.2906)
loss: tensor(4.0353)
loss: tensor(3.8134)
loss: tensor(3.6182)
loss: tensor(3.4456)
loss: tensor(3.2944)
loss: tensor(3.1646)

1
2
3
4
5
6
# 使用训练的模型对测试集进行预测
pred2 = net(X_test2.view(-1,1))
plt.figure(figsize=(10, 8))
plt.plot(X_test2.data.numpy(), y_test2.data.numpy(), 'o')
plt.plot(X_test2.data.numpy(), pred2.data.numpy())
plt.show()